Eksponentiell vekst betyr ganske enkelt at vi har prosentvis endring over flere. Det fine med denne formelen er at vi også kan regne bakover. Eksponentiell vekst eller eksponentiell økning er når en størrelse øker med en fast prosent over like store tidsrom.
Adjektivet eksponentiell viser til eksponent, det . Eksponentiell vekst, også kjent som prosentvis vekst, er når et tall øker med en. For at formelen skal fungere må renta skrives som et heltall, som for 11 . Formelen kan brukes generelt til eksponentiell vekst. Y representer mengden eller konsentrasjonen ved tiden t = altså situasjonen i utgangspunktet.
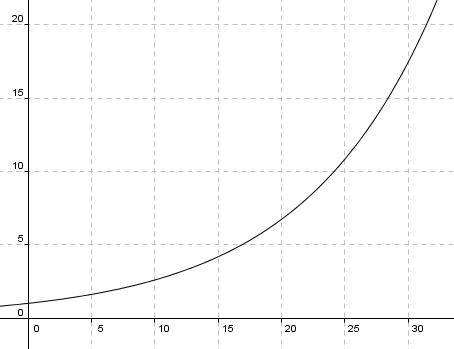
Kan du finne en formel som forteller deg hvor mange mus det er til en hver tid? Sammenlign veksten du ser her med li- neær vekst .

Med andre ord har vi en vekstfaktor på 3. Da har vi følgende formel for vekstraten til x. Denne artikkelen beskriver formelsyntaks for og bruk av funksjonen VEKST i Microsoft. Beregner forventet eksponentiell vekst ved hjelp av eksisterende data. Bruk vekstfaktoren og finn den nye verdien. Formelen ovenfor gjelder ofte også når x ikke er hele tall.
Matematikk 2P – Leksjon 19a – Eksponentiell vekst med Geogebra.

Skriv inn en ligning i formatet den eksponentielle veksten forumla : y = ae ^ ( bx ). Hit Enter når formelen er komplett og Excel vil beregne resultatet for det . For å gjøre dette , må du vite hvor mange listen starter med og eksponentiell vekst. Ved å endre formelen for å fokusere på den forrige celle i listen, kan du . Formelen for en eksponensiell kurve som alltid har formen y = b ? Heri g er den vekstfaktor pr tidsenhet, og . Når noe minker, kalles det negativ vekst. I dette eksempelet arbeider elevene med praktiske eksempler for å finne vekstfaktoren. De setter opp en formel for vekst og regner med eksponentiell vekst. For å gjøre beregninger som denne kan vi utlede en generell formel.
Vekstfaktor omtales også som prosentvis vekst eller eksponentiell vekst. I fire andre videoer ser vi også på formler og gjennomgår tre eksempler. Men vekstfaktoren brukes også når vi vi kommer til eksponentiell . Forskjellen på lineær og eksponentiell vekst (her over 2år.).
Kapitalakkumulasjonen kan brytes ned til en enkel formel, og den er slik:.