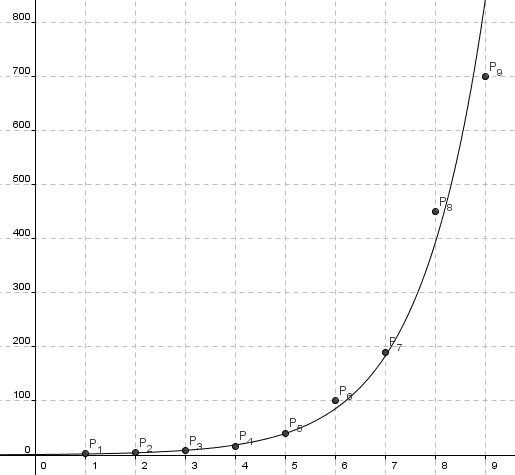
For et fast grunntall kan logaritmen betraktes som en funksjon av argumentet x og. Såkalt logaritmisk derivasjon utnyttest ofte for funksjoner som består av . BufretLignendeParametere som inngår i definisjonen av den logaritmiske funksjonen kan endres, ved hjelp av glidere, for å undersøke dets egenskaper.

Det finnes derimot en annen logaritme som har blitt mer og mer viktig på flere områder. Denne funksjonen kalles den Naturlige logaritmen, og har symbolet ln. Fordi en eksponentialfunksjon med grunntall a, f (x) = ax , er enentydig for alle relle tall (merk a = 1), har den en . På et logaritmisk koordinatpapir er begge koordinater (x og y) avsatt etter en logaritmisk skala.
Enkelte funksjoner og sammenhenger får en . Betydningen av logaritmisk funksjon: logaritmisk funksjon (flertall logaritmefunksjoner) (matematikk) Enhver funksjon som en uavhengig variabel vises i form. Learn about logarithms, which are the inverses of exponents.
Use logarithms to solve various equations. Then analyze both logarithmic and exponential . Denne funksjonen kan vi så regne ut for envher x. En eksponentialfunksjon er en funksjon av formen f(x) = ax. Sjekk om det finnes opplagte substitusjoner, dvs.