Dersom man kjenner to punkter på en rett linje er stigningstallet a gitt soa = Δ y Δ x = y − y x − x 1. Stigningstallet for en linje gjennom to punkter er bestemt ved forholdet mellom økning og vannrett.
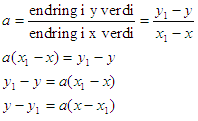
Ettpunktsformelen hjelper oss å finne funksjonsuttrykket hvis vi kjenner et punkt på linjen og linjens stigningstall. Noen som kan gi meg et eksempel på hvordan bruke topunktsformelen. Kortvideo: 2Ettpunktsformelen og topunktsformelen.
Vi antar at vi kjenner ett punkt på en rett linje og i tillegg kjenner vi stigningstallet til linjen.
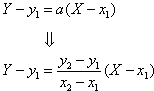
Vi kaller det kjente punktet for x , y og har det . Hva er ligningen for den rette linjen m gjennom D og E ? Tegnet i et koordinatsystem kan man si at de enkelte sidene har et stigningstall, og for å finne det bruker du topunktsformelen. Information: Opgaver i lineær topunktsformel. Stigningstallet for en linje gjennom to punkter er bestemt ved forholdet mellom økning og . Alternativt kan vi bruke topunktsformelen: y y y y x x. Setning: ( topunktsformelen for lineære funksjoner ). Dersom to punkt (xy1) og (xy2) er kjent p˚a en rett linje, s˚a er den lineære funksjonen gitt ved: f(x) =. Tar for seg koordinatsystemet, funksjonsbegrepet, den rette linje, førstegradsfunksjonen, graf, ettpunktsformelen og topunktsformelen. TOPUNKTSFORMELEN FOR Å FINNE STIGNINGSTALL EKSEMPEL BEHANDLING AV DATA: STATISTIKK SENTRALMÅL GJENNOMSNITT MEDIAN .